A glass of milk and a bucket of water

Puzzle. We have a glass of milk and a bucket of water (Fig. 1). We take a spoonful of milk from the glass and transfer it to the bucket. Then, we take a spoonful from the bucket and transfer it to the glass. Which will be greater, the amount of water in the glass or milk in the bucket? 

Answer. Equal 

Fig. 1 A glass of milk and a bucket of water.

Solution. The answer is surprising because we added a spoonful of milk to the bucket and transferred less than a spoonful of water to the glass. However, this spoon, which is partly filled with water, must also contain milk from the bucket to complete it. We use the same spoon for both actions. This guarantees that the amount of foreign liquid in the containers (water in the glass and milk in the bucket) will be equal.

I find the proof by contradiction most effective so that we will apply it here. Suppose the milk glass has more water than the water bucket has milk. This implies that the glass gained more liquid than it lost, increasing its volume. Conversely, the bucket received less than it lost, causing a decrease in the liquid volume. However, we used the same spoon in both transfers, so the liquid volume should stay unaffected. We arrived at the contradiction. Therefore, our original assumption is incorrect, and the amount of foreign liquid in the containers must be equal.

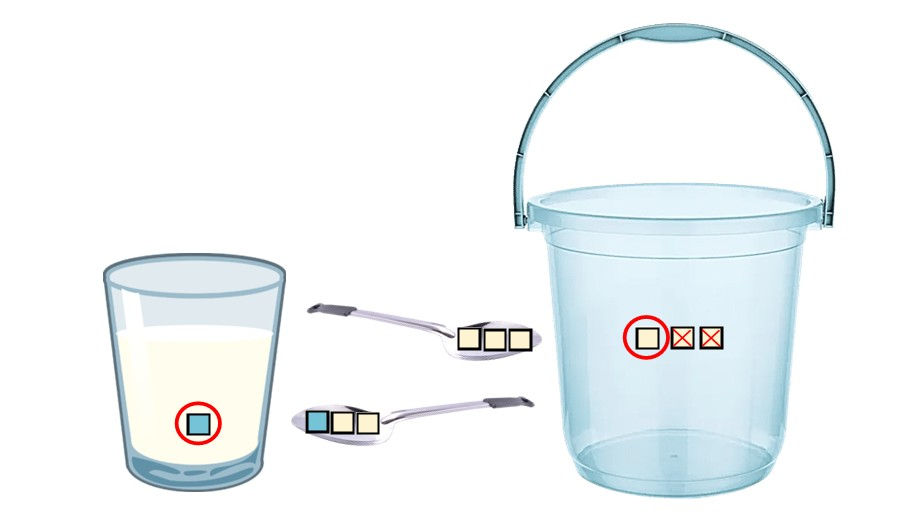
We can also use numbers to illustrate the answer. Let the spoon from the bucket contain 1/3 water and 2/3 milk (Fig. 2). Then, we removed 2/3 milk from the bucket, leaving behind 1/3 milk, and added 1/3 water to the glass. As a result, both containers end up with an equal amount of foreign liquid, circled in red: 1/3 water in the glass and 1/3 milk in the bucket.

Fig. 2 The milk glass has 1/3 water, and the water bucket has 1/3 milk after the back-and-forth liquid transfer.

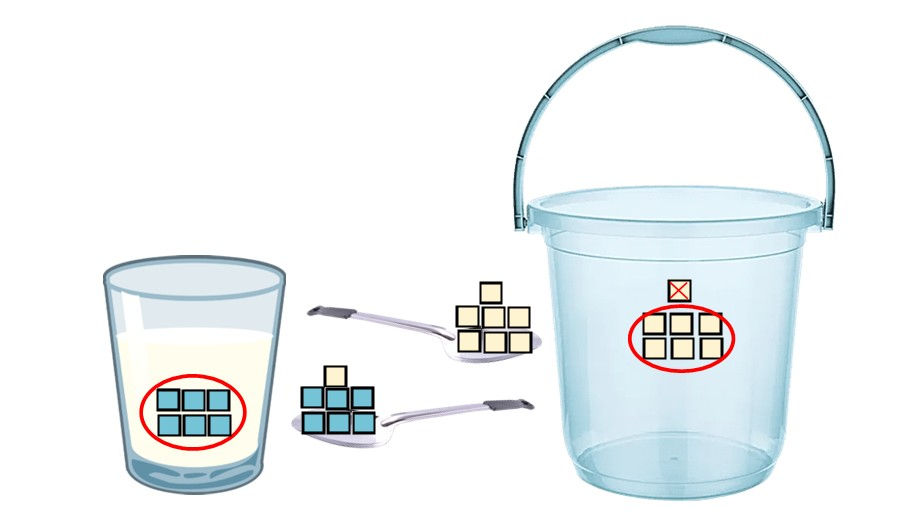
Let the spoon from the bucket hold 6/7 water and 1/7 milk (Fig. 3). Then, we removed 1/7 milk from the bucket, leaving 6/7 milk behind, and added 6/7 water to the glass. Consequently, both containers again end up with an equal amount of foreign liquid: 6/7 water in the glass and 6/7 milk in the bucket. The key is that what is native in one container becomes foreign in the other. So, the amount of local liquid (water) removed from the bucket will always match the amount of foreign liquid (milk) left behind.

Fig. 3 A spoon from the bucket adds 6/7 water to the glass, leaving 6/7 milk in the bucket.

It will make no difference whether we stir the bucket or not. If we scoop all the milk from the bucket, we transfer no water to the glass, leaving both containers free of foreign liquid. If we scoop no milk, a spoonful of water will be transferred to the glass, resulting in both containers having a spoonful of foreign liquid. We have already examined the scenario where the spoon is partly filled with milk and water.

The size of the containers is also irrelevant. The milk container can be larger than or the same size as the bucket. The crucial point is to use the same spoon for both actions, ensuring the amount of liquid transferred back and forth stays the same. Then:

3/3 milk (moved to bucket) = 1 full spoon = 2/3 milk + 1/3 water

and

7/7 milk = 1 spoon = 6/7 water + 1/7 milk